Fun with Letter Diamonds
A recent programming challenge appeared on The Social Programmer blog: http://www.craigmurphy.com/blog/?p=1417. The idea is to create a letter 'diamond' from any given starting letter. For example the diamonds for 'D' and 'E' are:
A
B B
C C
D D
C C
B B
A
A
B B
C C
D D
E E
D D
C C
B B
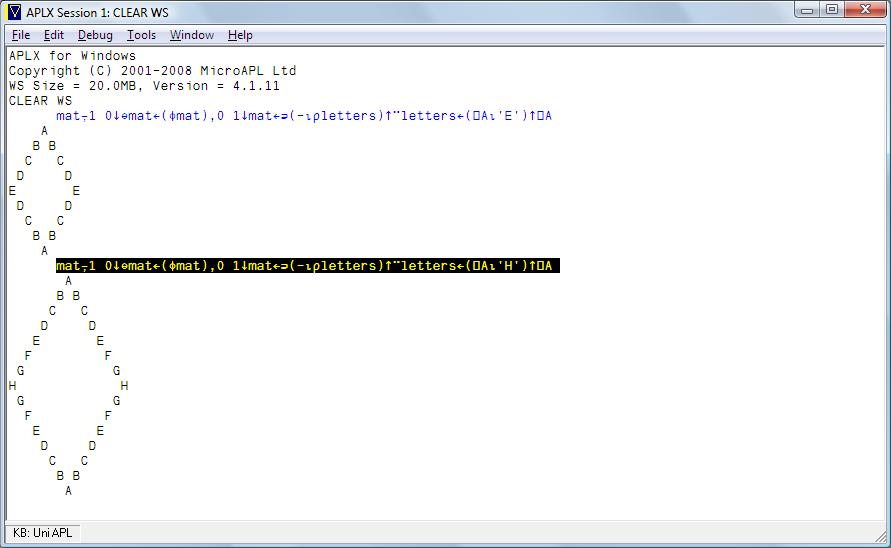
ASo far there have been entries in a number of computer languages, some of which run to many lines of code. In APL, the solution can be done in a single line:
mat⍪1 0↓⊖mat←(⌽mat),0 1↓mat←⊃(-⍳⍴letters)↑¨letters←(⎕A⍳'E')↑⎕A
A
B B
C C
D D
E E
D D
C C
B B
AI'm hoping that programmers new to APL will be intrigued and will want to explore further. You may not have an APL font installed, so here is a screenshot. If the code above doesn't look like the blue line in this screenshot you need to install a Unicode APL font before you can read the rest of this Wiki page.
To see how this works, it might be clearer to re-cast the code as a function returning an explicit result R:
∇R←LetterDiamond A;letters
[1] letters←(⎕A⍳A)↑⎕A ⍝ Get letters, e.g. A-E
[2] R←⊃(-⍳⍴letters)↑¨letters ⍝ Form upper-right side
[3] R←R⍪1 0↓⊖R←(⌽R),0 1↓R ⍝ Reflect to get whole diamond
∇
LetterDiamond 'E'
A
B B
C C
D D
E E
D D
C C
B B
ALine [1] just gets the letters from 'A' to 'E' (say):
letters←(⎕A⍳'E')↑⎕A
letters
ABCDE⎕A is the alphabet, ⎕A⍳'E' finds the position of 'E' in the alphabet (5) and 5↑⎕A gives the first five letters of the alphabet.
Line [2] forms the top right quadrant of the diamond:
R←⊃(-⍳⍴letters)↑¨letters
R
A
B
C
D
ETo break this down further, the expression -⍳⍴letters just produces the following negative numbers:
-⍳⍴letters ¯1 ¯2 ¯3 ¯4 ¯5
These numbers are used to perform a take (↑) on the letters, producing a nested vector in which each element is a character padded at the left by 0 to 4 spaces:
(-⍳⍴letters)↑¨letters
A B C D E
⎕DISPLAY (-⍳⍴letters)↑¨letters
┌→──────────────────────────────┐
│ ┌→┐ ┌→─┐ ┌→──┐ ┌→───┐ ┌→────┐ │
│ │A│ │ B│ │ C│ │ D│ │ E│ │
│ └─┘ └──┘ └───┘ └────┘ └─────┘ │
└∊──────────────────────────────┘
⍝ This is the equivalent to doing:
(¯1↑'A')(¯2↑'B')(¯3↑'C')(¯4↑'D')(¯5↑'E')
A B C D EFinally the disclose ⊃ function converts this into a matrix.
Line [3] is responsible for forming the final diamond. First we use the reverse ⌽ function to flip the array horizontally:
⌽R
A
B
C
D
E
(⌽R),R
AA
B B
C C
D D
E E
(⌽R),0 1↓R
A
B B
C C
D D
E EFinally we repeat the process to flip the array vertically using the first axis rotate ⊖ and form the final result:
R⍪1 0↓⊖R←(⌽R),0 1↓R
A
B B
C C
D D
E E
D D
C C
B B
AIf you want to learn more about APL or try running the code in an APL interpreter, see the APL Tutorial on this Wiki.
Author: SimonMarsden
 APL Wiki
APL Wiki