|
Size: 1603
Comment:
|
Size: 5803
Comment: Under construction
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 5: | Line 5: |
| `FitUtil` is a Dyalog Unicode Workspace (v14.1) that contains useful functions related to curve fitting using the domino operator (`⌹`). The results are shown in plain text in the session and graphically using WPF. The regressions performed are: | `FitUtil` is a Dyalog Unicode Workspace (v14.1) that contains useful functions related to curve fitting. The regressions performed are: |
| Line 19: | Line 19: |
| The first 9 curve fittings are a least square fit using the APL's domino operator. The Weibull regression is obtained by iterations and may not converge to a solution all the time.<<BR>> | The first 9 curve fittings are a least square fit using the APL's domino operator (`⌹`). The Weibull regression is obtained by iterations and may not converge to a solution all the time.<<BR>> |
| Line 22: | Line 22: |
| The function `TFIT` will removed the non-significatives points by performing a Student test on the data. | The function `TFIT` will removed the non significant points by performing a Student test on the data. |
| Line 26: | Line 26: |
| `FIT` and `TFIT` will present the results of the curve fittings in the APL session, the function SHOW will present them graphically using `∆FIT` or `∆TFIT`. It uses WPF and the Syncfusion libraries. | `FIT` and `TFIT` will present the results of the curve fittings in the APL session, the function SHOW will present them graphically using the variables `∆FIT` or `∆TFIT`. It uses WPF and the Syncfusion libraries. |
| Line 30: | Line 30: |
| x FIT y SHOW ∆FIT |
x FIT y ⍝ Normal regression |
| Line 33: | Line 32: |
| x TFIT y SHOW ∆TFIT |
x TFIT y ⍝ Will remove the non significant points before performing the regressions |
| Line 36: | Line 35: |
| For example for the following values of X1 and Y1: {{{ X1 0.5497 0.817 0.999 1.19 2.78 5.53 10.21 16.59 22.56 99.7 200 1000 1500 5000 Y1 19.191 17.672 17.063 16.613 14.602 13.25 12.418 11.859 11.512 9.75 9.008 7.309 6.836 5.765 }}} The following is written in the session: {{{ X1 FIT Y1 ------------------------------------------------------------------------------------------ CALCULATION OF THE CORRELATION'S COEFFICIENTS ------------------------------------------------------------------------------------------ 1. LINEAR: Y' = 13.454 + ¯0.0019732×X (r² = 0.388) 2. EXPONENTIAL: Y' = 12.989 × exp(¯0.00020156×X) (r² = 0.522) 3. POWER: Y' = 17.034 × X*¯0.12515 (r² = 0.996) 4. LOGARITHMIC: Y' = 16.631 + ¯1.3954×ln(X) (r² = 0.963) 5. PARABOLIC: Y' = 14.235 + ¯0.0077116×X + 0.0000012078×X*2 (r² = 0.599) 6. CUBIC: Regression not possible 7. LINEAR @(0,0): Y' = 0 + 0.0017639×X (r² = 0.000) 8. PARABOLIC @(0,0): Y' = 0 + 0.096933×X + ¯0.000020817×X*2 (r² = 0.000) 9. CUBIC @(0,0): Y' = 0 + 0.46267×X + ¯0.00044524×X*2 + 7.0616E¯8×X*3 (r² = 0.000) 10.WEIBULL: Y' = 0.34555 × exp(3.9069 × X*¯0.036282) (r² = 0.996) ------------------------------------------------------------------------------------------ THE BEST REGRESSION IS No 3: POWER ------------------------------------------------------------------------------------------ }}} With the following WPF Window will be showing the results graphically: {{attachment:FIT.png || width=1220}} To remove the non significant points before doing the regressions: {{{ X1 TFIT Y1 ------------------------------------------------------------------------------------------ SAME REGRESSIONS WITH THE NON SIGNIFICANT POINT(S) REMOVED: ------------------------------------------------------------------------------------------ 1. LINEAR: Y' = 12.746 + ¯0.0013976×X (r² = 0.871) The Following Points were Removed: 1 2 3 4 10 11 12 13 2. EXPONENTIAL: Y' = 12.706 × exp(¯0.00015817×X) (r² = 0.936) The Following Points were Removed: 1 2 3 4 10 11 12 13 3. POWER: Y' = 17.09 × X*¯0.12548 (r² = 0.999) The Following Points were Removed: 1 5 6 7 11 4. LOGARITHMIC: Y' = 16.703 + ¯1.3586×ln(X) (r² = 0.990) The Following Points were Removed: 1 2 5 6 7 8 9 5. PARABOLIC: Y' = 13.39 + ¯0.0061933×X + 9.3462E¯7×X*2 (r² = 0.953) The Following Points were Removed: 1 2 3 4 8 9 10 11 6. CUBIC: Regression Not possible 7. LINEAR @(0,0): Y' = 0 + 0.0016421×X (r² = 0.000) The Following Points were Removed: 1 2 3 4 5 6 7 8 9 10 11 8. PARABOLIC @(0,0): Y' = 0 + 0.4465×X + ¯0.000089216×X*2 (r² = 0.000) The Following Points were Removed: 12 13 9. CUBIC @(0,0): Y' = 0 + 8.3272×X + ¯0.40538×X*2 + 0.000080744×X*3 (r² = 0.000) The Following Points were Removed: 10 11 12 13 10.WEIBULL: Y' = 0.025474 × exp(6.5082 × X*¯0.020864) (r² = 0.999) The Following Points were Removed: 1 5 6 9 10 11 ------------------------------------------------------------------------------------------ THE BEST REGRESSION IS No 10: WEIBULL ------------------------------------------------------------------------------------------ }}} With the following WPF Window will be showing the results graphically: {{attachment:TFIT.png || width=1220}} This Workspace is also a demonstration of how to: 1. Use Syncfusion's !SfChart to show the Plot. 1. Customize the Look of the Tabs. 1. Capture a screen and save it to disk. 1. Capture a screen and print it. == How to download FitUtil == 1. Download [[attachment:FitUtil.dws]] == Version Information == {{{ February 2016 - Initial version (1.0) }}} == Version Information == ||Original author: ||Pierre Gilbert || ||Responsible: ||PierreGilbert || ||Email: || <<MailTo(apgil AT SPAMFREE videotron DOT ca)>> || ---- CategoryDyalog - CategoryDyalogDotNet - CategoryDyalogWpfUtilities - CategoryDotNet |
UNDER CONSTRUCTION |
FitUtil
Overview
FitUtil is a Dyalog Unicode Workspace (v14.1) that contains useful functions related to curve fitting. The regressions performed are:
1. Linear: Y' = a + b×X 2. Exponential: Y' = a × exp(b×X) 3. Power: Y' = a × X*b 4. Logarithmic: Y' = a + b×ln(X) 5. Parabolic: Y' = a + b×X + c×X*2 6. Cubic: Y' = a + b×X + c×X*2 + d×X*3 7. Linear through origin: Y' = 0 + b×X 8. Parabolic through origin: Y' = 0 + b×X + c×X*2 9. Cubic through origin: Y' = 0 + b×X + c×X*2 + d×X*3 10. Weibull: Y' = a × exp(b×X*c)
The first 9 curve fittings are a least square fit using the APL's domino operator (⌹). The Weibull regression is obtained by iterations and may not converge to a solution all the time.
The main functions are FIT and TFIT. Both will perform 10 different curve fittings on a set of X and Y values.
The function TFIT will removed the non significant points by performing a Student test on the data.
The results are stored in a global nested variable called ∆FIT or ∆TFIT depending of the main function used.
FIT and TFIT will present the results of the curve fittings in the APL session, the function SHOW will present them graphically using the variables ∆FIT or ∆TFIT. It uses WPF and the Syncfusion libraries.
The usage of the functions is as follow:
x FIT y ⍝ Normal regression
x TFIT y ⍝ Will remove the non significant points before performing the regressionsFor example for the following values of X1 and Y1:
X1
0.5497 0.817 0.999 1.19 2.78 5.53 10.21 16.59 22.56 99.7 200 1000 1500 5000
Y1
19.191 17.672 17.063 16.613 14.602 13.25 12.418 11.859 11.512 9.75 9.008 7.309 6.836 5.765The following is written in the session:
X1 FIT Y1 ------------------------------------------------------------------------------------------ CALCULATION OF THE CORRELATION'S COEFFICIENTS ------------------------------------------------------------------------------------------ 1. LINEAR: Y' = 13.454 + ¯0.0019732×X (r² = 0.388) 2. EXPONENTIAL: Y' = 12.989 × exp(¯0.00020156×X) (r² = 0.522) 3. POWER: Y' = 17.034 × X*¯0.12515 (r² = 0.996) 4. LOGARITHMIC: Y' = 16.631 + ¯1.3954×ln(X) (r² = 0.963) 5. PARABOLIC: Y' = 14.235 + ¯0.0077116×X + 0.0000012078×X*2 (r² = 0.599) 6. CUBIC: Regression not possible 7. LINEAR @(0,0): Y' = 0 + 0.0017639×X (r² = 0.000) 8. PARABOLIC @(0,0): Y' = 0 + 0.096933×X + ¯0.000020817×X*2 (r² = 0.000) 9. CUBIC @(0,0): Y' = 0 + 0.46267×X + ¯0.00044524×X*2 + 7.0616E¯8×X*3 (r² = 0.000) 10.WEIBULL: Y' = 0.34555 × exp(3.9069 × X*¯0.036282) (r² = 0.996) ------------------------------------------------------------------------------------------ THE BEST REGRESSION IS No 3: POWER ------------------------------------------------------------------------------------------
With the following WPF Window will be showing the results graphically: 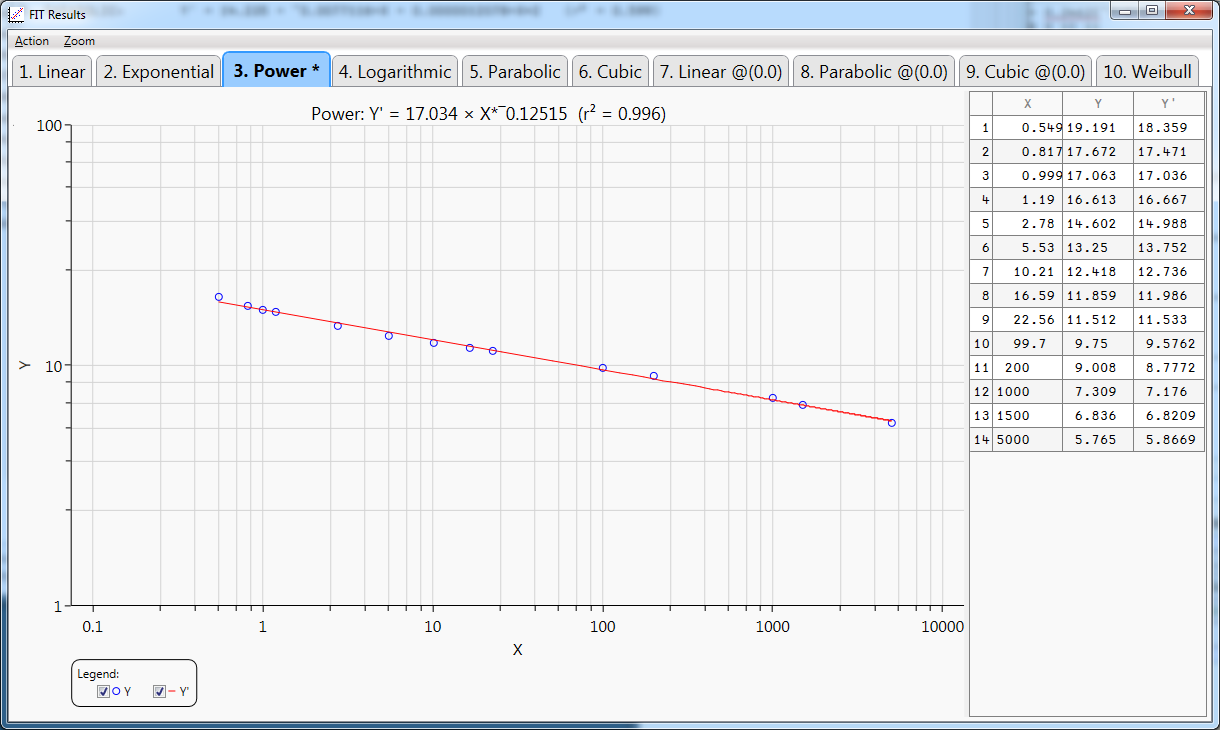
To remove the non significant points before doing the regressions:
X1 TFIT Y1
------------------------------------------------------------------------------------------
SAME REGRESSIONS WITH THE NON SIGNIFICANT POINT(S) REMOVED:
------------------------------------------------------------------------------------------
1. LINEAR: Y' = 12.746 + ¯0.0013976×X (r² = 0.871)
The Following Points were Removed: 1 2 3 4 10 11 12 13
2. EXPONENTIAL: Y' = 12.706 × exp(¯0.00015817×X) (r² = 0.936)
The Following Points were Removed: 1 2 3 4 10 11 12 13
3. POWER: Y' = 17.09 × X*¯0.12548 (r² = 0.999)
The Following Points were Removed: 1 5 6 7 11
4. LOGARITHMIC: Y' = 16.703 + ¯1.3586×ln(X) (r² = 0.990)
The Following Points were Removed: 1 2 5 6 7 8 9
5. PARABOLIC: Y' = 13.39 + ¯0.0061933×X + 9.3462E¯7×X*2 (r² = 0.953)
The Following Points were Removed: 1 2 3 4 8 9 10 11
6. CUBIC: Regression Not possible
7. LINEAR @(0,0): Y' = 0 + 0.0016421×X (r² = 0.000)
The Following Points were Removed: 1 2 3 4 5 6 7 8 9 10 11
8. PARABOLIC @(0,0): Y' = 0 + 0.4465×X + ¯0.000089216×X*2 (r² = 0.000)
The Following Points were Removed: 12 13
9. CUBIC @(0,0): Y' = 0 + 8.3272×X + ¯0.40538×X*2 + 0.000080744×X*3 (r² = 0.000)
The Following Points were Removed: 10 11 12 13
10.WEIBULL: Y' = 0.025474 × exp(6.5082 × X*¯0.020864) (r² = 0.999)
The Following Points were Removed: 1 5 6 9 10 11
------------------------------------------------------------------------------------------
THE BEST REGRESSION IS No 10: WEIBULL
------------------------------------------------------------------------------------------With the following WPF Window will be showing the results graphically: 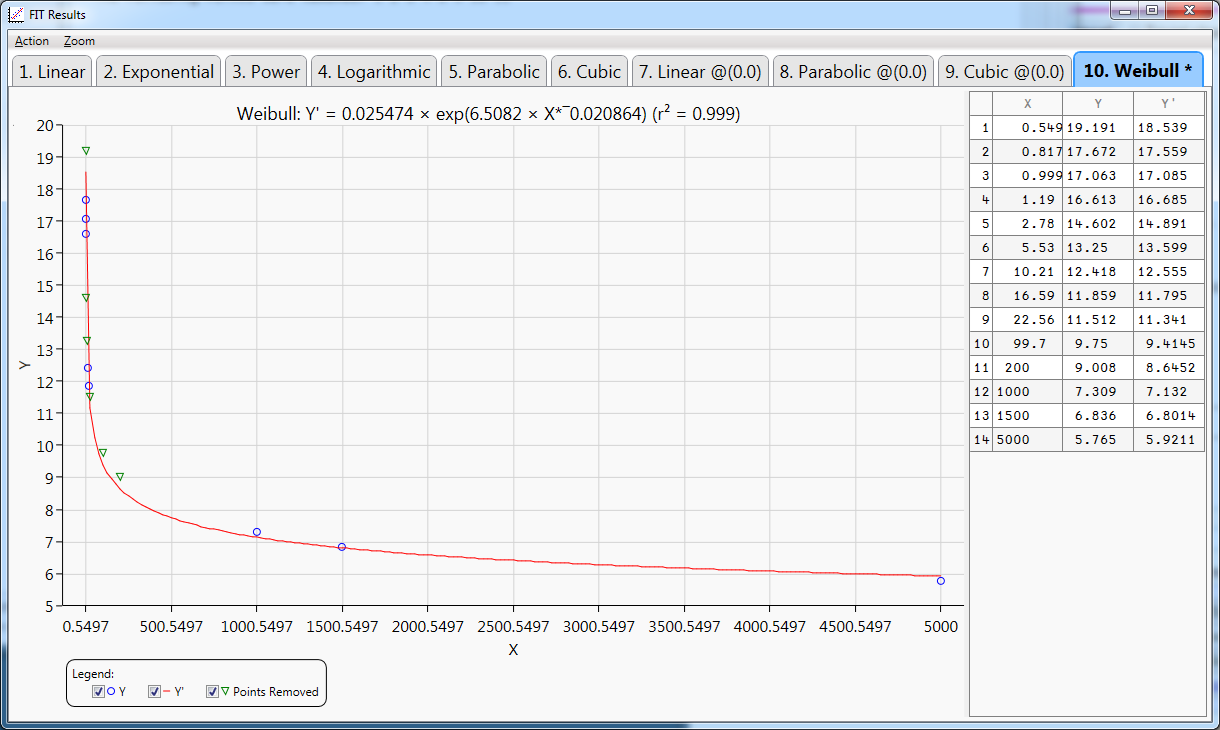
This Workspace is also a demonstration of how to:
Use Syncfusion's SfChart to show the Plot.
- Customize the Look of the Tabs.
- Capture a screen and save it to disk.
- Capture a screen and print it.
How to download FitUtil
Download FitUtil.dws
Version Information
February 2016 - Initial version (1.0)
Version Information
Original author: |
Pierre Gilbert |
Responsible: |
|
Email: |
<apgil AT SPAMFREE videotron DOT ca> |
CategoryDyalog - CategoryDyalogDotNet - CategoryDyalogWpfUtilities - CategoryDotNet
 APL Wiki
APL Wiki