|
Size: 6136
Comment: Added example of drawing a bitmap
|
Size: 7034
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 96: | Line 96: |
| 'win.picture' ⎕wi 'new' 'picture'('align' ¯1) 'win.picture' ⎕wi 'bitmap'(~(Spiral X)∊Primes N*X) |
'win.picture' ⎕WI 'new' 'picture'('align' ¯1) 'win.picture' ⎕WI 'bitmap'(~(Spiral X)∊Primes N*X) |
| Line 209: | Line 209: |
| As an extra here is an extended version of Spiral (by DanB) that accepts non square matrices: {{{ ∇ R←Spiral N;col;direction;indices;repeat;row;start;t;tr;⎕IO [1] ⍝ Build a spiralling list of integers into an N[×M] matrix [2] ⎕IO←1 [3] tr←>/(row col)←2⍴N [4] (row col)←tr⌽row col ⍝ work on wide matrices [5] start←(2|row)+t+col×t←⌊row÷2 ⍝ where the 1st element will be [6] repeat←,(t+col-row),[1.1]t←⍳row [7] indices←+\(row×col)↑start,repeat/(2×row)⍴1,(-col),¯1,col [8] R←⍋indices [9] R←(1+tr,~tr)⍉row col⍴R ⍝ restore order [10] →tr↓0 ⋄ R←⌽R ⍝ correct direction ∇ }}} with an example {{{ Spiral 6 4 11 10 9 24 12 1 8 23 13 2 7 22 14 3 6 21 15 4 5 20 16 17 18 19 }}} |
|
| Line 211: | Line 237: |
| ---- |
Ulam's Spiral of Prime Numbers
Contents
About Ulam's Spiral
The Polish mathematician Stanisław Ulam discovered an interesting way of viewing the distribution of prime numbers, now known as an Ulam Spiral.
Imagine writing down a spiral of numbers which starts with '1' in the centre and then spirals outwards:
37 36 35 34 33 32 31 38 17 16 15 14 13 30 39 18 5 4 3 12 29 40 19 6 1 2 11 28 41 20 7 8 9 10 27 42 21 22 23 24 25 26 43 44 45 ...etc
Now put a circle around each prime number and look at the pattern produced. You might expect to get a random distribution, but instead the primes seem to line up along diagonal lines. Here, for example, is the 20 x 20 spiral with prime number positions indicated by '○' characters:
○ ○ ○
○ ○ ○ ○
○ ○ ○ ○
○ ○ ○
○ ○ ○
○ ○ ○ ○
○ ○ ○
○ ○ ○ ○ ○ ○
○ ○ ○ ○ ○ ○
○ ○ ○
○ ○ ○○ ○ ○ ○
○ ○ ○
○ ○
○ ○ ○ ○ ○ ○
○ ○ ○ ○ ○
○ ○
○ ○ ○ ○ ○
○ ○
○ ○ ○
○ ○ ○ ○
Ulam's Spiral in APL
We can generate Ulam spirals in APL using two simple functions. The first of these is based on the Sieve of Eratosthenes and generates prime numbers:
∇R←Primes N
[1] R←(2=+⌿0=(⍳N)∘.|⍳N)/⍳N
∇ The second function generates a spiral pattern:
∇R←Spiral N;start;indices;⎕IO
[1] ⎕IO←1
[2] start←(2|N)+(N+1)×⌊N÷2
[3] indices←+\(N*2)↑start,(2/⍳N)/(2×N)⍴1 (-N) ¯1 N
[4] R[indices]←R←⍳⍴indices
[5] R←(N,N)⍴R
∇ Together we can use them to generate Ulam spirals:
X←7 ⍝ Choose a small size so it fits easily on Wiki page
Primes X*2
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
Spiral X
37 36 35 34 33 32 31
38 17 16 15 14 13 30
39 18 5 4 3 12 29
40 19 6 1 2 11 28
41 20 7 8 9 10 27
42 21 22 23 24 25 26
43 44 45 46 47 48 49
' ○'[⎕IO+(Spiral X)∊Primes X*2]
○ ○
○ ○
○ ○ ○
○ ○○
○ ○
○
○ ○Large patterns get too big to display in this form. Instead we can display the spiral in a window:
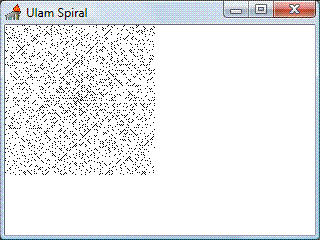
You can do this in APLX using the following code. Other APLs allow something similar.
'win' ⎕WI 'new' 'window'('title' 'Ulam Spiral')
'win.picture' ⎕WI 'new' 'picture'('align' ¯1)
'win.picture' ⎕WI 'bitmap'(~(Spiral X)∊Primes N*X)
How the APL code works
The function to generate prime numbers is discussed fully here: Sieve of Eratosthenes
To understand the Spiral function, start by considering the following 7 x 7 spiral:
37 36 35 34 33 32 31 38 17 16 15 14 13 30 39 18 5 4 3 12 29 40 19 6 1 2 11 28 41 20 7 8 9 10 27 42 21 22 23 24 25 26 43 44 45 46 47 48 49
If you were to walk this spiral you would start in the middle, then go right one, up one, left two, down two, etc. Suppose we use the following representation:
1 |
Right |
¯7 |
Up |
¯1 |
Left |
7 |
Down |
Using this representation, we would walk the spiral using the following steps:
1 ¯7 ¯1 ¯1 7 7 1 1 1 ¯7 ¯7 ¯7 ¯1 ¯1 ¯1 ¯1 7 7 7 7 1 1 1 1 1 ¯7 ¯7 ¯7 ¯7 ¯7 ...etc
Using parentheses makes the pattern clearer: (1),(¯7),(¯1,¯1),(7,7),(1,1,1),(¯7,¯7,¯7) etc
We can generate this pattern in APL using the following expression:
N←7
2/⍳N
1 1 2 2 3 3 4 4 5 5 6 6 7 7
(2/⍳N)/(2×N)⍴1 (-N) ¯1 N
1 ¯7 ¯1 ¯1 7 7 1 1 1 ¯7 ¯7 ¯7 ¯1 ¯1 ¯1 ¯1 7 7 7 7 1 1 1 1 1 ¯7 ¯7 ¯7 ¯7 ¯7 ...etcNow consider the index positions of the elements of the 7 x 7 grid:
(N,N)⍴⍳N*2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
If we were to start the walk in the middle and follow the same outward spiral, we would encounter the numbers in the following order: 25 26 19 18 17 24 31 32 33 34 27 20 13 12 11 10 9 16 23 etc. Notice that we get this sequence by starting with '25' and then successively adding each number in the sequence 1 ¯7 ¯1 ¯1 7 7 1 1 1...
First of all we need to find the number at the middle. We need to consider grids where N is odd and even:
start←(2|N)+(N+1)×⌊N÷2
start
25We use this to generate the sequence of index positions:
indices←+\(N*2)↑start,(2/⍳N)/(2×N)⍴1 (-N) ¯1 N
indices
25 26 19 18 17 24 31 32 33 34 27 20 13 12 11 10 9 16 23...To finish the Spiral function, we use selective assignment to put a '1' in index position '25', a '2' in position '26', etc, and reshape the result to a 7 x 7 grid:
R[indices]←R←⍳⍴indices
R←(N,N)⍴R
R
37 36 35 34 33 32 31
38 17 16 15 14 13 30
39 18 5 4 3 12 29
40 19 6 1 2 11 28
41 20 7 8 9 10 27
42 21 22 23 24 25 26
43 44 45 46 47 48 49
Now we're ready to use the Prime and Spiral functions to generate a spiral of primes, putting a '1' wherever we find a prime number.
(Spiral X)∊Primes X*2 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 0 0 1 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0
Finally, we can replace 1 and 0 by '○' and a blank space to make the pattern easier to see:
' ○'[⎕IO+(Spiral X)∊Primes X*2] ○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ○ ○
As an extra here is an extended version of Spiral (by DanB) that accepts non square matrices:
∇ R←Spiral N;col;direction;indices;repeat;row;start;t;tr;⎕IO
[1] ⍝ Build a spiralling list of integers into an N[×M] matrix
[2] ⎕IO←1
[3] tr←>/(row col)←2⍴N
[4] (row col)←tr⌽row col ⍝ work on wide matrices
[5] start←(2|row)+t+col×t←⌊row÷2 ⍝ where the 1st element will be
[6] repeat←,(t+col-row),[1.1]t←⍳row
[7] indices←+\(row×col)↑start,repeat/(2×row)⍴1,(-col),¯1,col
[8] R←⍋indices
[9] R←(1+tr,~tr)⍉row col⍴R ⍝ restore order
[10] →tr↓0 ⋄ R←⌽R ⍝ correct direction
∇with an example
Spiral 6 4 11 10 9 24 12 1 8 23 13 2 7 22 14 3 6 21 15 4 5 20 16 17 18 19
Author: SimonMarsden
 APL Wiki
APL Wiki