A simple animation of Conway's Game of Life

A one line APL expression to calculate successive generations in Conway's Game of Life can be found here.

For a bit of fun, let's take the APL expression and display its output in a window, with a 1 second pause between generations.

Here's an example function using APLX (not under development any more) ; this example will work on Windows, Macintosh and Linux:

      ∇nextGeneration←Life currentGeneration
[1]  ⍝⍝ Take a matrix of Booleans and returns one
[2]   nextGeneration←⊃↑1 currentGeneration∨.^3 4=+/,¯1 0 1∘.⊖¯1 0 1∘.⌽⊂
      currentGeneration
      ∇
 
      ∇Animate gen;win
[1]   win←'⎕' ⎕NEW 'window'
[2]   win.title←'Game of Life'
[3]   win.picture.New 'picture'
[4]   win.picture.align←¯1
[5]   win.picture.imagesize←10×⍴gen
[6]   win.OnClose←'→0'
[7]   win.Show
[8]   :Repeat
[9]     win.picture.bitmap←~10/10⌿gen
[10]    gen←Life gen
[11]    0 0⍴⎕WE 1
[12]  :EndRepeat
      ∇

The Animate function makes use of two system classes, 'Window' and 'Picture'. It sets the picture to fill the whole window (align ¯1) and sets a callback to execute when the window's close button is clicked (→0). It then loops to display each generation as a bitmap using a 10x10 block for each cell.

Here is a sample pattern known as a pulsar, which oscillates between three generations

      ⍝ Upper-left quadrant of pulsar
      pulsar←¯8 ¯8 ↑ 6 6⍴0 0 1 1 0 0 0 0 0 1 1 0 1 0 0 1 0 1 1 1 1 0 1 1 0 1 0 1 0 1 0 0 1 1 1 0

      ⍝ Fill in other quadrants
      pulsar←pulsar∨⊖pulsar←pulsar∨⌽pulsar←17 17 ↑pulsar

      ⍝ Start the animation
      Animate pulsar

Here's a screen snapshot of the three generations:

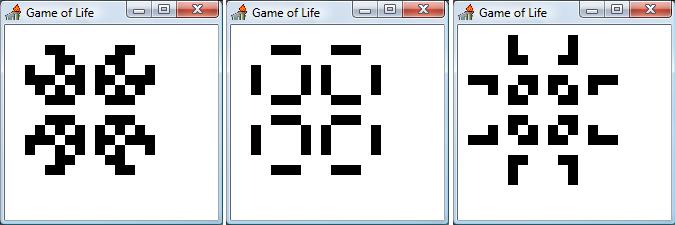
Here's another sample pattern which starts off only one row high but grows indefinitely.

      ⍝ One row pattern
      gun←0 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 0 0 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 0 0 0 0

      ⍝ Use a big grid to see how it evolves
      grid←50 50⍴0
      grid[25;]←50↑grid
      Animate grid

Here's a screenshot showing various stages of the pattern's evolution

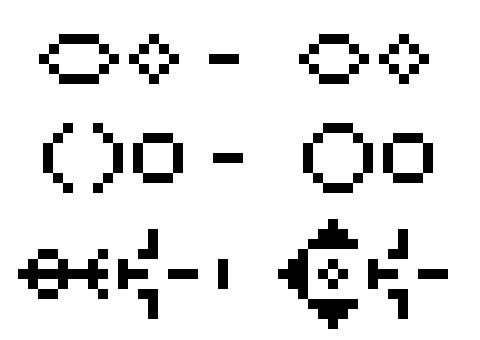
Author: SimonMarsden

CategoryShowCases